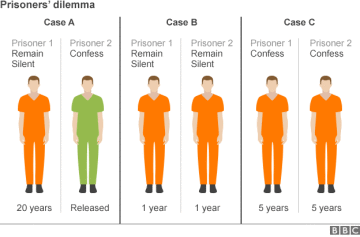
Před pár dny jsme v práci hráli takovou hru. Třeba ji znáte. Říká se jí Vězňovo dilema. V průběhu nám vyvstala zajímavá otázka:
Podrazit parťáka, když to je logicky nejvýhodnější krok? Nebo naopak chtít pomoct za každou cenu a tím trpět na úkor druhého?
Zkusím v rychlosti hru projít na 2 příkladech a pár věcí si na tom ukázat.
Kdo sbalí blondýnku?
Viděli jste někdy film A Beautiful Mind, který vypráví příběh matematika Johna Nashe? John chtěl podobné “hry” a úlohy řešit obecným, a hlavně správným způsobem. (Celému odvětví aplikované matematiky, která se tím zabývá, se říká Teorie Her.) V následujícím videu je úryvek z filmu, kde John s kamarády řeší, jak sbalit blondýnku v hloučku kamarádek:
Scéna z filmu a Beautiful Mind
V této scéně přišel John na jednu zásadní věc. Pokud by všichni chtěli dostat blondýnku, o kterou usilovali, nejspíš by zůstali bez přítelkyně. Když to převedu do Teorie her, pokud by každý hráč maximalizoval pouze svoje zisky, celkový součet zisků bude menší, než kdyby důvěřovali ostatním a udělali by pro sebe trochu méně. Tím by všichni získali více.
Pojďme si to spočítat
Představme si: Stojíte před automatem, na druhé straně je váš protihráč, a oba můžete nebo nemusíte do automatu hodit minci. Když ji tam hodíte, na druhé straně vypadnou 3 mince. Když ji tam nehodíte, nic se nestane. Oba se rozhodujete najednou a nemůžete se domlouvat. Co uděláte? Hodíte minci nebo ne? Nechte si chvilku na promyšlení, a až budete vědět, co chcete udělat, pokračujte.
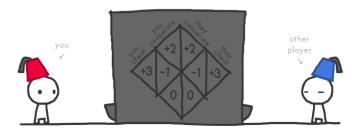
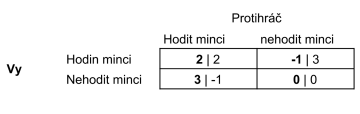
Ať protihráč hodí nebo ne, vždy pro mě bude výhodnější nic neházet. Dejme tomu, že protihráč hodí minci (levý sloupec tabulky), tudíž dostanu 3 zlaťáky. Kdybych hodil zlaťák i já, jednu minci ztratím, takže mám pouze 3-1=2. Když protihráč minci nehodí (pravý sloupec tabulky), opět je pro mě výhodnější minci nehodit, protože nic neztratím.
Pokud by oba hráči hráli logicky a v každém kroku by se snažili maximalizovat svůj zisk, hra brzy přestane být zajímavá, protože oba hráči nebudou do automatu minci házet. (Tomuto bodu se právě říká Nashovo Equilibrium.)
Co se stane, když hru změníme na vícekolovou a budeme hrát proti více hráčům? Cílem najednou bude nejen porazit aktuálního protihráče, ale maximalizovat můj celkový zisk. (Pokud vás hra zajímá, projděte si skvělý web, zabere cca 30 minut a ukáže hravou formou více strategií.)
Závěrem
Nebudu zabíhat do velkých detailů (záleží také, jak přesně namodelujeme hru, jaké jsou jednotlivé hodnoty: zisky, prohry, pravděpodobnosti).
Nicméně v podobných hrách je nejúspěšnější ten hráč, který opakuje protihráče, a zároveň umí odpouštět.
To znamená, že dlouhodobě si nenechá šikanu líbit, ale zároveň chybu protihráče umí odpustit. Není to náhodou podobné i v životě a byznysu?
Přijde mi zajímavá skutečnost, jak se mění nejlepší strategie podle toho, čeho chce hráč dosáhnout. Pokud chce hráč jen za každou cenu vyhrát, dlouhodobě se mu to nebude dařit na úkor někoho jiného.
A to zažíváme často i v práci. Přece jenom je lepší snažit se dlouhodobě bojovat o WIN-WIN stavy, než krátkodobě vyhrát na úkor druhých.
Hezký den a zkuste třeba dneska někomu odpustit. :)





